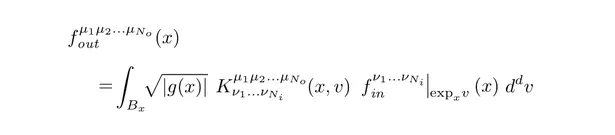Maurice Weiler
Deep Learning Researcher
Welcome!
My name is Maurice Weiler and I’m a researcher working on geometric deep learning.
Education: I received my PhD from the University of Amsterdam, supervised by Max Welling. Prior to my doctorate, I obtained a Master's degree in computational and theoretical physics from Heidelberg University. For more details, have a look at my CV.
Research: My research deals with incorporating geometric inductive priors into deep neural networks.
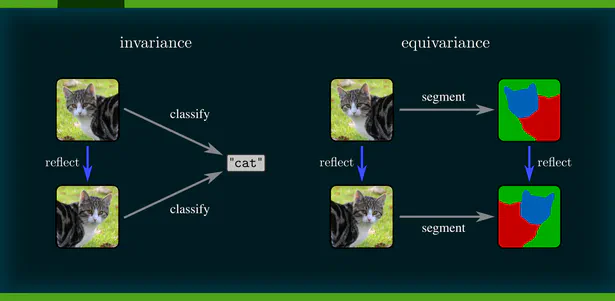
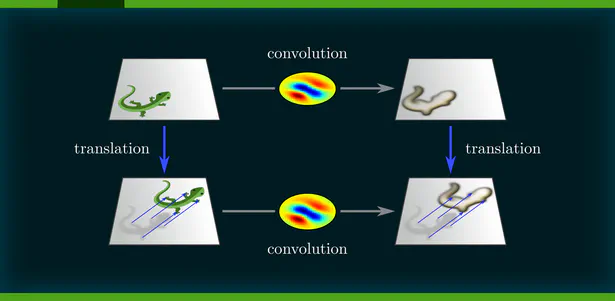
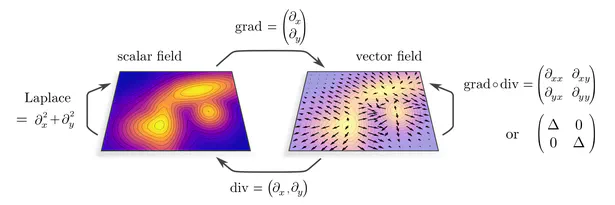
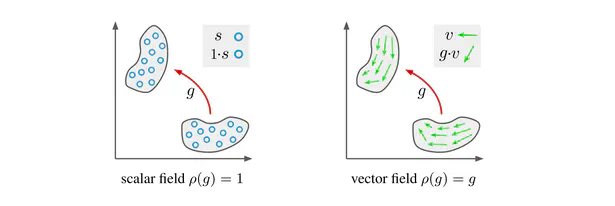
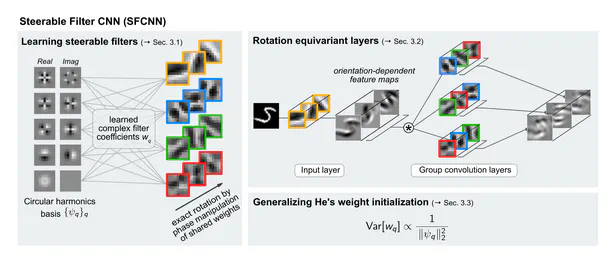
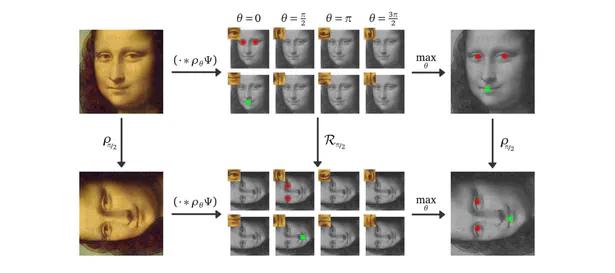
A primary focus of my work is on the design of Equivariant Convolutional Neural Networks (CNNs). These are geometry-aware neural networks that are constrained to commute with geometric transformations of feature vector fields. Equivariance ensures consistent predictions across transformed inputs, which leads to a greatly enhanced data efficiency, robustness and interpretability.
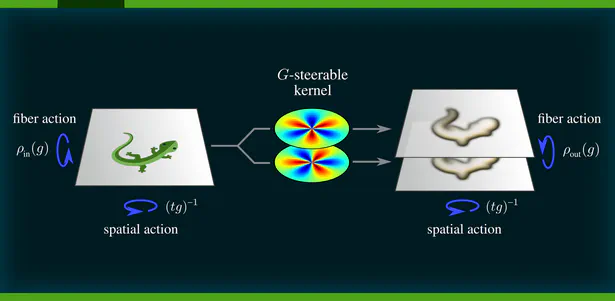
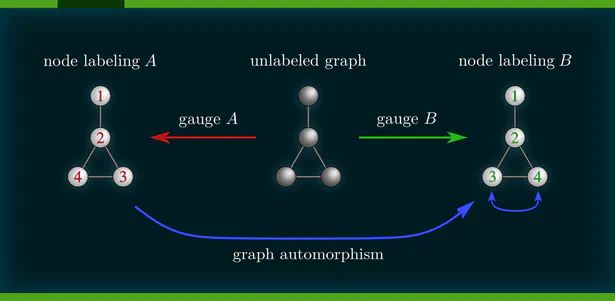
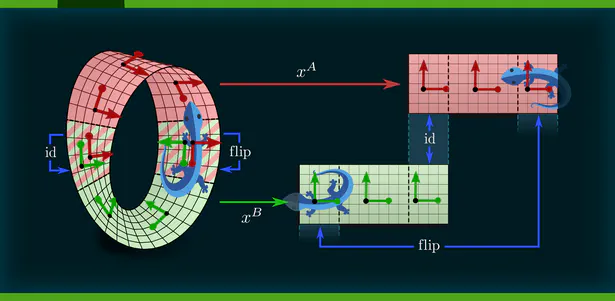
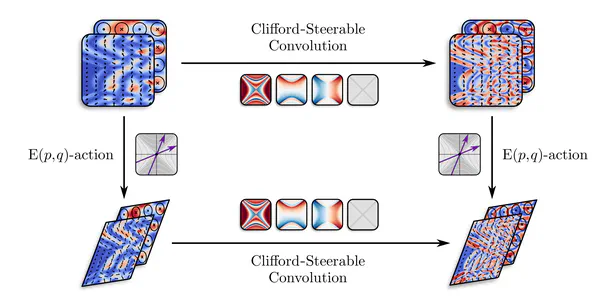
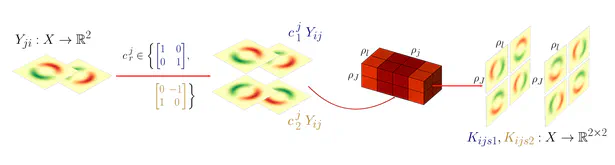
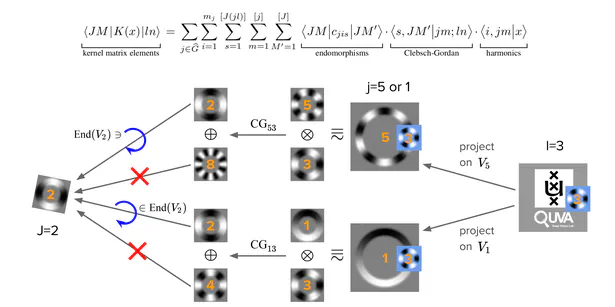
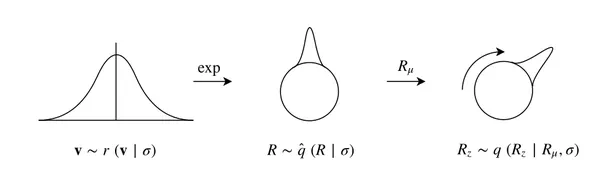
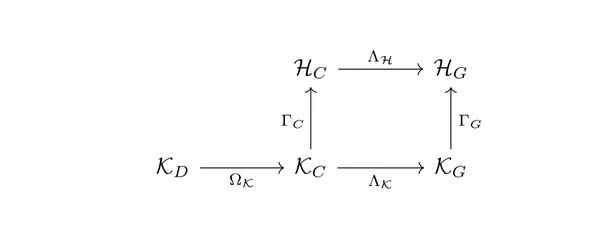
During my PhD, I developed a quite general representation theoretic formulation of equivariant CNNs , applying to a wide range of spaces, symmetry groups and group actions. My research showed that equivariant convolutions generally require $G$-steerable kernels , which are symmetry-constrained convolution kernels that are related to quantum representation operators . The endeavor to generalize CNNs to Riemannian manifolds led me to a gauge field theory of convolutional networks which constitutes a paradigm shift from global symmetries to local gauge transformations. Our PyTorch library escnn found use in a variety of applications, ranging from biomedical and satellite image processing to tasks in environmental, chemical and material sciences, or in reinforcement learning and robotics.
If you would like to learn more about my research on equivariant CNNs, please have a look at our book "Equivariant and Coordinate Independent CNNs" and check out my blog posts and publications.
Further interests: Besides my core research topics, I am more broadly interested in generative models, graph neural networks, non-Euclidean embedding methods, PDE-inspired deep models, and deep learning for the physical sciences.
In my freetime I enjoy climbing, hiking, MTBing, cooking, playing strategic games and DJing.
Book publication
+ PhD Thesis
+ PhD Thesis

Equivariant and Coordinate Independent Convolutional Networks
A Gauge Field Theory of Neural Networks
This monograph brings together our findings on the representation theory and differential geometry of equivariant CNNs that we have obtained in recent years. It generalizes previous results, presents novel insights, and adds background knowledge, intuitive explanations, visualizations and examples.
The version linked above is a pre-release of my PhD thesis. A printed edition from an academic publisher will soon be available as well.
A brief overview of the content:- The first part develops the representation theory of equivariant CNNs on Euclidean spaces. It demonstrates how the layers of conventional and generalized CNNs are derived purely from symmetry principles. Popular models – including group convolutional networks, harmonic networks, and tensor field networks – are unified in a common mathematical framework.
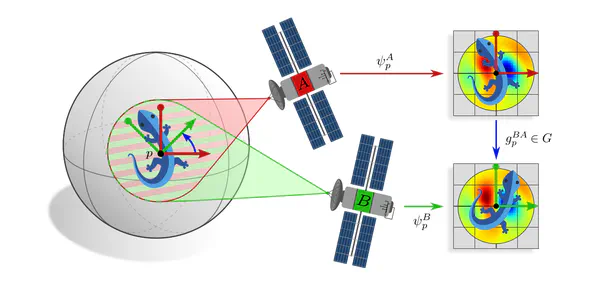
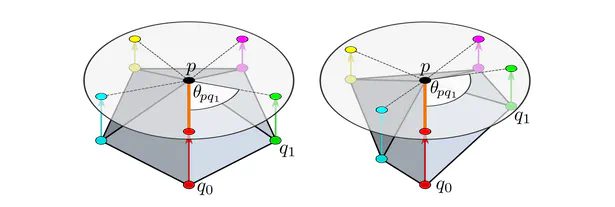
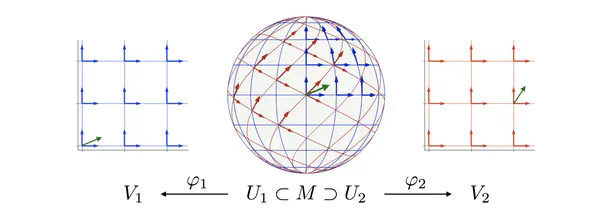
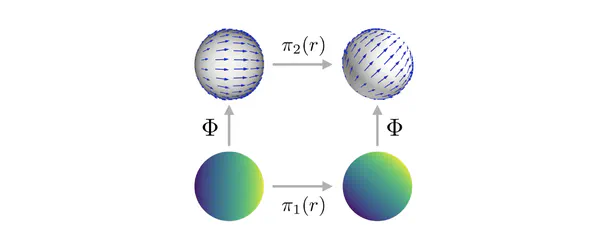
- We subsequently extended this formulation to Riemannian manifolds. The requirement for coordinate independence is shown to result in gauge symmetry constraints on the neural connectivity. Part 2 of the book gives an intuitive introduction to CNNs on manifolds. Part 3 formalizes these ideas in the language of associated fiber bundles.
- The fourth part is devoted to applications and instantiations on specific manifolds. It revisits Euclidean CNNs from the differential geometric perspective and covers spherical CNNs and CNNs on general surfaces.
For more details, see the table of contents, read the abstract, intro and outline, or have a look at the list of theorems. Reveal the book's back cover by clicking on its image above. on the left. You should also check out the associated series of blog posts, which explains key concepts and insights in an easily understandable language.