Abstract
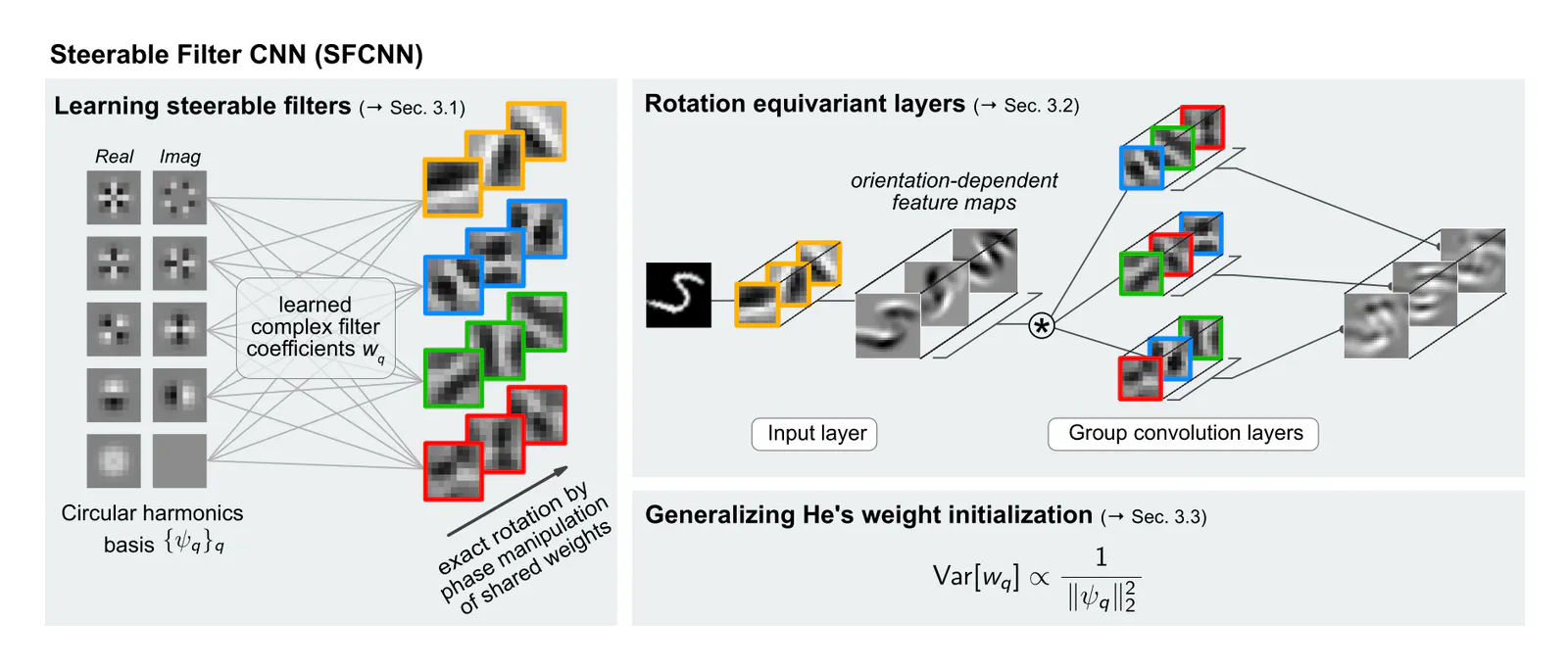
In many machine learning tasks it is desirable that a model’s prediction transforms in an equivariant way under transformations of its input. Convolutional neural networks (CNNs) implement translational equivariance by construction; for other transformations, however, they are compelled to learn the proper mapping. In this work, we develop Steerable Filter CNNs (SFCNNs) which achieve joint equivariance under translations and rotations by design. The proposed architecture employs steerable filters to efficiently compute orientation dependent responses for many orientations without suffering interpolation artifacts from filter rotation. We utilize group convolutions which guarantee an equivariant mapping. In addition, we generalize He’s weight initialization scheme to filters which are defined as a linear combination of a system of atomic filters. Numerical experiments show a substantial enhancement of the sample complexity with a growing number of sampled filter orientations and confirm that the network generalizes learned patterns over orientations. The proposed approach achieves state-of-the-art on the rotated MNIST benchmark and on the ISBI 2012 2D EM segmentation challenge.
Maurice Weiler
Deep Learning Researcher
I’m a researcher working on geometric and equivariant deep learning.