Abstract
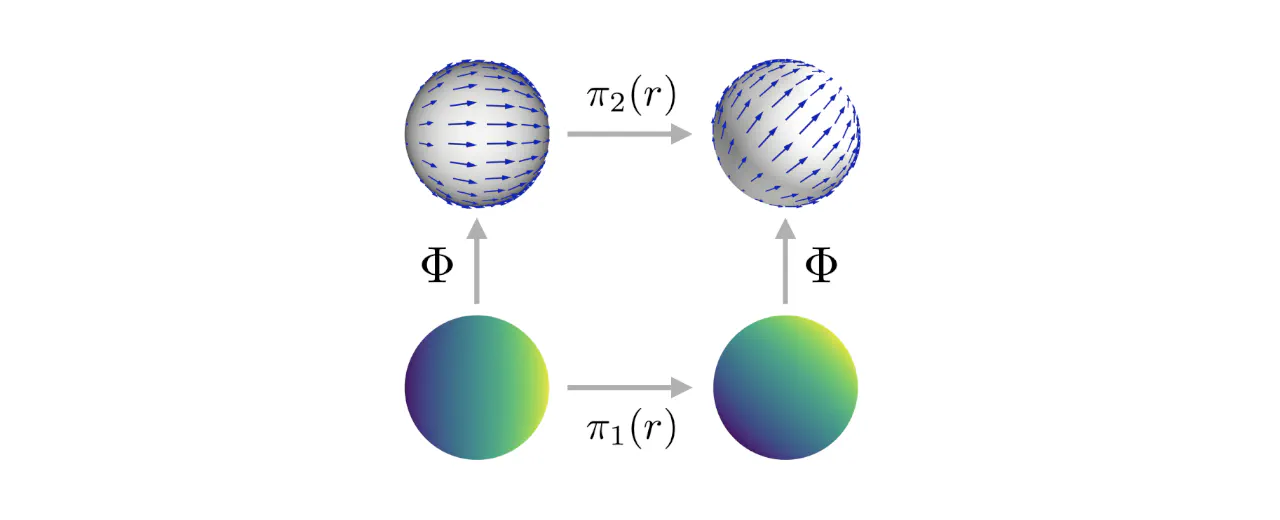
We present a general theory of Group equivariant Convolutional Neural Networks (G-CNNs) on homogeneous spaces such as Euclidean space and the sphere. Feature maps in these networks represent fields on a homogeneous base space, and layers are equivariant maps between spaces of fields. The theory enables a systematic classification of all existing G-CNNs in terms of their symmetry group, base space, and field type. We also consider a fundamental question: what is the most general kind of equivariant linear map between feature spaces (fields) of given types? Following Mackey, we show that such maps correspond one-to-one with convolutions using equivariant kernels, and characterize the space of such kernels.
Maurice Weiler
Deep Learning Researcher
I’m a researcher working on geometric and equivariant deep learning.